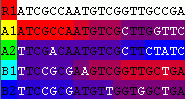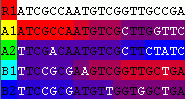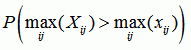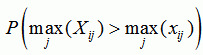Recco - Recombination Analysis Using Cost Optimization
Make sure to read the Walkthrough Guide - it summarizes my experience using Recco!
Contents
- Download and Installation
- The Graphical User Interface
- Main View
- Alignment View
- The P-Value Inspector - How to Keep Complexity at Bay
- File Menu
- View Menu
- Settings Menu
- Mutation Cost
- Gap Cost
- Command-line Arguments
1. Download and Installation
Recco was tested with Java 1.4.2 and 1.5.0, but might also work with older versions of Java. Please download and install the Java Runtime Environment, if you do not have it already.
- proceed to the download page, accept the licence agreement and download the .zip file.
- unzip to some directory and enter the directory.
- type java -jar Recco.jar on the command line prompt to start Recco, or double-click the file recco.bat on Microsoft Windows based systems.
2. The Graphical User Interface
2.1 Main View
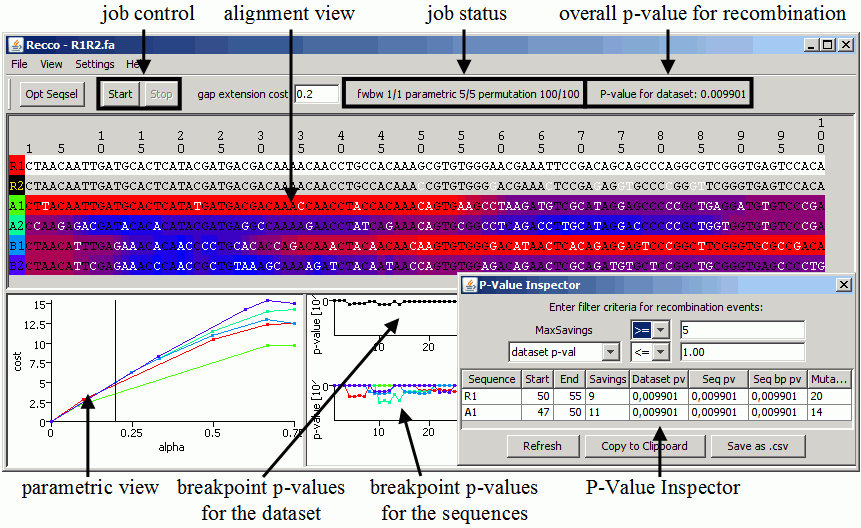
An example of the output of Recco for the dataset R1R2.fa. Description:
- job control: (re-)start and stop running analyses. Also available in the menu.
- job status: displays the current computation status
- parametric x/y: there are x jobs finished of a total of y jobs for the parametric cost curves, where y=number of selected sequences
- fwbw denotes the job performing the forward-backward analysis (i.e. cip and rip)
- permutation represents the jobs for computing p-values
- Opt Seqsel: removes sequences from the dataset such that the evidence for recombination of the currently selected putative recombinant is maximized. In the alignment shown, for example, R1 and R2 are very similar to each other. If R1 is the putative recombinant, clicking Opt Seqsel removes R2 such that the recombination event is visible. Use this feature with caution as it can result in false positives.
- overall p-value for recombination: shows the p-value for recombination for the whole dataset.
- parametric view: shows the parametric cost curves for each sequence with the respective color. The current setting for alpha is shown as a vertical black line and can be changed by clicking inside the chart. The linear segments of a cost curve from left to right each corresond to one optimal solution with increasing amounts of recombination. Even though the cost curves can be useful for the analysis, the p-value inspector is easier to use.
- breakpoint p-values for the sequences: shows the p-value for recombination at each position per sequence. Depending on your setting in the view menu, the breakpoint p-values for no, one or all sequences are shown. If only one sequence should be visualized, the putative recombinant sequence (for details, see alignment view) is visualized.
- breakpoint p-values for the dataset: shows the p-value for recombination at each position for the whole dataset.
- left clicking in either of the breakpoint charts centers the corresponding nucleotide position in the alignment view.
Most results are visualized interactively by the GUI. View setting (in the view menu) usually affect the display immediately, while settings affecting the computation (in the settings menu or in the alignment or parametric view) update the results and schedule new computation jobs. These jobs are then immediately processed, if autostart is enabled.
2.2 Alignment View
The alignment view falls into three parts, the names, the sequences and the positions. The name component has the following tasks:
- excluding/including sequences to the analysis:
- => right click (or hold control while left-clicking) on a sequence name to remove/add a sequence from/to the analysis.
- selecting the putative recombinant
(the sequence itself is shown with a white background)
- => left click on a sequence name
The position and sequences component do not accept mouse input. The sequences component shows either (depending on the setting in the view menu):
- optimal solution
- the sequence strips that are part of an optimal explanation of the putative recombinant are shown with a red background.
- cost measure cip
- the color of a nucleotide visualizes the total cost of an explanation forced through that nucleotide
- red is low cost and blue is high cost. Bright red nucleotides visualizes the optimal solution as in 1.
- robustness measure rip
- the color of a nucleotide visualizes the robustness score.
- red
- breakpoint p-values
- does not refer to an optimal solution (!) and is not very helpful
- red visualizes low (=more significant) p-values, blue visualizes high p-values
The computation of the optimal solution always refers to a setting of alpha as shown e.g. in the parametric view. A white foreground color in the alignment view highlights mutations with respect to the putative recombinant sequence.
Examples:
The following image shows cip with R1 as the putative recombinant and R2 excluded from the analysis:

The same analysis result as obtained by selecting View=>Optimal Solution Only:

2.3 P-Value Inspector - How to Keep Complexity at Bay
You can find a lot more information on how to use the P-Value Inspector in the Walkthrough Guide.
The P-Value Inspector condenses the information of an analysis and displays the discovered recombination events. It is only shown if View=>Show P-Value Inspector is selected:
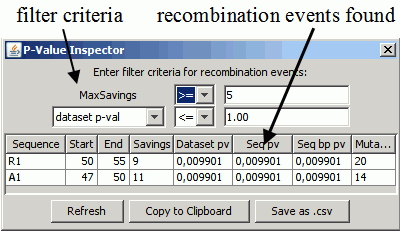
The table shows the recombination events in the dataset that satisfy the filter criteria. Each row in the table describes a single recombination event. For more details on the computation of the p-values, see the paper and the following section..
- Sequence: which sequence is a recombinant? => R1
- Start/End: the range of nucleotide positions where a recombination breakpoint could occur. => 49, 50, 51, 52, 53.
- Savings: the amount of mutation cost saved by introducing this recombination. In this example, the recombination led to a solution with 12 fewer mutations.
- Dataset pv: the p-value of this recombination event regarding the savings distribution over the whole dataset - a very conservative measure for recombination.
- Seq pv: the p-value of this recombination event regarding the savings distribution over R1 - use this if you analyze a single sequence only, e.g. for subtying.
- Seq bp pv: the p-value of this recombination event regarding the savings distribution a single breakpoint - not conservative enough for practical use.
Selecting a row (i.e. a recombination event): visualizes the recombination in the alignment view by setting the sequence and alpha value accordingly and centering the breakpoint position in the alignment view.
Other actions of the P-value Inspector:
- Change the filter criteria
- Savings >= 5 has shown to work well in practice as it filters noise
- You may want to relax the filter on the p-value to display and analyze weak recombination signals manually.
- If you enter a new bound, you have to confirm your input by pressing ENTER, or refresh the table by clicking "Refresh".
- Refresh: refreshes the table of recombination events. This is done automatically if the computation is finished or if you select a different filter criteria.
- Copy to Clipboard: copies the contents of the table to the system clipboard, using a TAB-delimited format compatible with Microsoft™ Excel®.
- Save as .csv: saves the contents of the table as a comma-separated file.
2.3.1 How P-Values are Computed
The following exposition is for anybody that wants to know what happens behind the scene. You can savely skip this section.
Recco computes p-values for recombination in the whole dataset, for each sequence, at each position, and at each position for a specific sequence. The p-values are based on sij, the amount of mutation cost that can be saved by allowing for recombination at position i in the explanation of sequence j. By permuting the columns of the alignment and recomputing sij for the permuted dataset, we can estimate the distribution of sij under the null-hypothesis of no recombination. Now let Xij be the random variable (i.e. distribution) for sij under the null-hypothesis and xij be the values for the unpermuted dataset. Then we define:
| p-value for the whole dataset |
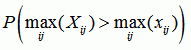 |
| p-value for sequence j |
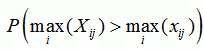 |
| p-value for position i |
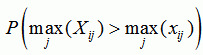 |
| p-value for position i and sequence j |
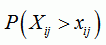 |
In the following, we focus on a single recombination event. We define a recombination event as some interval i1 ≤ i ≤ i2 for some sequence j where c := xij has a constant value. We then assign to each recombination event the following p-values:
dataset p-value
the p-value for recombination in the dataset if the recombination event was the strongest in the whole dataset |
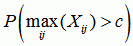 |
sequence p-value
the p-value for recombination in the sequence if the recombination event was the strongest in the sequence |
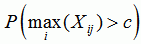 |
sequence breakpoint p-value
the median of the p-values for sequence j and any position between i1 and i2. Please use this value as an indicator only, as it is statistically hard to justify taking the median of some p-values |
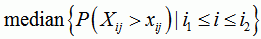 |
2.4 File Menu
This is pretty self-explanatory:
- Open Alignment...: Opens a FASTA file containing a multiple sequence alignment.
- Open Analysis...: Opens a file that has been saved by "Save Analysis As...".
- Permute Dataset...: permutes the columns of the alignment and effectively destroys recombination signals. Mainly for illustrative purposes.
- Save Analysis As...: Stops all currently running jobs and saves the alignment, input parameters and all results computed so far to a file. The file might not be readable by the next version of Recco.
- Save Analysis as Text...: Saves the result of the parametric analysis and the p-values to a human-readable text file, so that the results can be imported into a spreadsheet program like Excel.
- Print...: prints the optimal solution currenlty shown in the alignment view to a PDF-File. May result in a huge file, though.
2.5 View Menu
This menu is rather self-explanatory and changes how and which data is visualized. Be sure to enable Show P-value Inspector.
2.6 Settings Menu
Besides the "Stop Computation" menu item, greyed out menu items are not implemented. The settings menu is used to change the following input parameters:
- Autostart: if autostart is enabled, changes in the input parameters immediately start a new batch of jobs to update the results.
- Mutation Cost: see below for details.
- Recombination Cost: there is only one recombination cost model, delta dirac, which assigns a cost of 1 to every recombination.
- Gap Cost: see below for details.
- Number of Permutations...: you can set the number of permutations for computing p-values here. The higher, the more accurate are the p-values and the lower the p-values can be.
- Load/Save Settings: loads/saves all settings in the view and settings menu.
- Maximum Alpha for Permutations...: this setting has to be used with extreme caution, as a value lower or equal to 2/3 may result in p-values that are inaccurate. However, it can also result in a significant speed increase. The idea is to restrict the cost curves that are computed during the permutation analysis to the range [0, maxAlpha]. The cost curves are then used to compute the feature MaxSavings. The distribution of MaxSavings for the permutations and its value for the original dataset define the p-value for a dataset or a sequence. Restricting the analysis to [0, maxAlpha] also restricts the feature MaxSavings, so that it is either larger than (1-maxAlpha)/maxAlpha or set to zero. The p-value for datasets or sequences with a low MaxSavings value are thus too low (i.e. too significant). The same reasoning holds for the p-values for breakpoint detection. It is important to keep in mind, that only breakpoints, datasets and sequences with a low MaxSavings value, i.e. with a low preference for recombination (roughly speaking), get wrong p-values. Thus, it can be a useful tool for quickly scanning a dataset for recombination.
2.6.1 Mutation Cost
The mutation cost m(a, b) defines the cost of matching a character a with a character b. Gaps '-' and unknown characters 'N', '?' are treated like any other character in the algorithm. Therefore, it is important to set the associated costs carefully. For example, we can avoid pairing gaps preferentially if we set the mutation cost m(-, a)=0 for any character a.
Predefined mutation cost matrices include:
- Hamming: m(a,a) = 0 for any a and m(a,b) = 1 for any a != b.
- DNA: m(a,b) = Hamming(a,b) for any a and b in {A, C, G, T} and m(a,b) = 0 if either a or b is a gap or unkown character. This treats gaps and unknown characters as no information, i.e. as a matching character.
- BLOSUM62: uses the inverted BLOSUM62 matrix, with the exception that a substitution involving a gap has a cost of 0.
- PAM250: uses the inverted PAM250 matrix, with the exception that a substitution involving a gap has a cost of 0.
Additionally, it is possible to create, load and save user defined mutation matrices by selecting the "User defined..." menu option. The file format is a pure text file and straigth-forward to adapt.
2.6.2 Gap Cost
As we use a multiple alignment including gaps as an input, we have to decide how to score gaps. Consider this example:
recombinant AC----GT----CTGGTAGCGCT
explanation ACGAGCCT----CCT----GCGC
The upper sequence shows the (putative) recombinant that we seek to explain by recombination and mutation. The explanation is the sequence that is obtained by recombination of the other sequences in the alignment. In our case, there are three different kinds of gaps (in order of appearance in the alignment above):
- a gap in the recombinant
As our goal is to explain the recombinant, this gap is only discarding information we do not need. As such it should only involve low or zero costs.
- a gap in the recombinant and the explanation
This setting is a result of using a multiple alignment as input and does not constitute a real gap. Incorporating a paired gap in the solution does not involve any cost.
- a gap in the explanation
An interpretation of this gap is that we do not have information to explain part of the recombinant. Consequently, it should be scored with a rather high cost.
In the gap cost dialog you can assign gap extension costs for gaps of type 1 or type 3 seperately. Biologicall, the cost for gaps of type 1 should be very small - a cost of 0 is appropriate, therefore. The cost for gaps of type 3 can also easily be changed in the toolbar, in case you need to experiment with it.
Gap open costs have been disabled as the permutation test for computing p-values reports wrong results in this case.
3 Command-line arguments
Recco runs an interactive GUI only if no command-line arguments are specified. A help text is displayed if you specify a single or an invalid command-line argument. The output format is the same as for the "Save Analysis as Text..." menu item.